オリンピックが始まったそうな。でもオレはテレビ持っていないので今回も蚊帳の外。そしたらお友達から長嶋さんが聖火リレーに出てたって聞いて、ワーオなんてタイムリーなんだろうって思ったんです。
言わずと知れた元巨人軍三塁手長嶋茂雄さん。所謂ひとつの〜セコムしてますか〜って何言ってるのかわからない長嶋茂雄さん。ジェネレーションを問わず多くの人に愛される長嶋茂雄さん。何故長嶋さんだけ特別なのだろう? そしてもう一人同じ匂いを放つ特別な人、ジョンレノン。オレの中では二人ともに白い、特別、清い、信用って印象がある。もちろんその時代を生きてない今の人たちが、全く同じ印象をもっているわけではないけれど、総じてこの二人を悪く言う人って、ほんと少ないと思うんです。今回はこのことと、言語と、寿命が、グルーっと巡りめぐって一続きしてるって話を書いてみようと思います。
まずは、『長嶋茂雄 』、『ジョン・レノン 』、『正規分布 』この三つのキーワードを解説します。
〜正規分布〜
『正規分布またはガウス分布は、確率論や統計学で用いられる連続的な変数に関する確率分布の一つである。データが平均値の付近に集積するような分布を表す。』
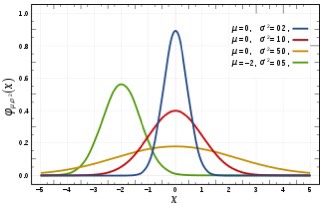
画像_正規分布
ちょー簡単に言うと、この(立体)世界で起こることを分析すると、どんな現象もこのグラフのような分布になってしまうって意味です。、、なんで?、、理由はこう。
分析する生物って人類だけですよね。ミミズが正規分布とか言わないでしょ。ネコだって言いません。人類だけ!じゃあその人類の特徴は?、、大脳皮質が発達してます。頭だけで一時記憶し、そのデータに基づき予測や次に起こることを計算できます。そしてその機能を使って言語を操ることが可能です。
つまりそれは言語機能に行き着きます。
じゃあ言語機能って?
言語とは体を使わなくても、現象(見たことや知ったこと)を言葉に変えることで、脳だけで一時記憶できる能力のこと。だから人は例えば音楽の一部を一時記憶できる時間が4秒だけなんです。音質は簡単に言葉に変換できないから。
この一時記憶能力を紡いだ状態が文章。所謂「てにをは」。一時記憶したデータを時系列に紡ぎ「何がどうしてどうなった」と経過や過程を表現できます。そしてこれが「時間」。だから時間は言語が紡いでる。
また時間が無いと脳内自我は意味を知ることができない。それは自分自身が意味を知るために、自分で時間を発生させているということなのです。
つまり正規分布という情報処理は、人類の脳内で起こる時間発生能動でもある。だからこの時間発生能動を考えてみます。この正規分布を何かの言葉で置き換えると、、
記憶階層
1 2 3…
スタイリッシュ(形状)
/
おしゃれー色合い(色相)
\
風合い(質感)
同じ「おしゃれ」に類する言葉でも大きく3つに分かれています。接続境界面そのものを表すスタイリッシュ。接続境界面の色相を表す色合い。接続境界面質を表す風合い。全て視覚刺激を表現する言語です。
例えば色合いにフォーカスしてみます。最新型スポーツカーを想像してください。深い黄色のボディに黒の外装パーツ。めっちゃ派手な車ですね。とここまでの想像はオレが色を指定しただけです。でも皆さんはそれなりに想像力を働かせ、こんな感じの想像したんじゃないかしらん。

画像_黄色のスポーツカー
でもそれは色相と形状での平均的想像ですね。色合いを言っただけなのに、車って条件から、ボディの質を金属製、パーツの質を樹脂或いは金属製って限定してますよね? 当たり前だけど、ボディが芋羊羹でできた車じゃ走れないですね。その場合黒のパーツは小豆の羊羹ですかね。
この平均的想像は脳内にある、或いは体から直ぐにもってこられる常時記憶を紡いで構成したのです。そしてこの時点では未だ時間を発生させていません。だってそれぞれの脳内で想像しただけですから。
でもこれを、例えば試作して、または設計図描いて、どこかの車メーカーに営業したとします。それは現実として行動したということ。すると脳内だけのことが現象になります。そこで時間を発生させたわけです。
同様に、このデザインの車に纏わる小説を書いたとします。これも時間(時系列)を発生させています。
つまり「人の脳は、何かの出力をする時、時間(時系列)を発生させるのです」。
因みにこの想像力を最大限活かして作った時系列こそ芸術です。つまり芸術は現象を変える力があるんです。
そして正規分布とは、現象に於ける局在のことです。それは3d。だから正規分布には時間が含まれている。もっと言えば、ある特定条件下の時間進行の最も多い要素を表している。それがトレンドや流行り、人気、経済的piの伸び率などと数値化できるわけです。
話変わり長嶋茂雄という生き神さまを考察します。
〜長嶋茂雄語録〜
・「I live in TOKYO」を過去形は「I live in EDO」。
・初のアメリカでマクドナルドを見て「アメリカにも進出してるんだなー」と言った。
・新車を購入したが、すぐに調子が悪いとメーカーに苦情を言ったが、サイドブレーキを引いたままだった。
・長嶋さんと同じ誕生日なんです。とファンに言われ「へ〜、で、貴方の誕生日はいつ?」と質問。
・監督復帰の記者会見時「僕は12年間漏電していたんですよ」。
・犬の散歩に行くといつも迷子になり、犬だけ帰ってくる。
・好きな番号は何ですか?の問いに「ラッキーセブンの3!」と即答。
・自分の車を上野駅にエンジンを掛けたまま放置。タクシーで帰ってきた。
・他人の100円玉を持ち帰り、後日「ごめん、俺の100円玉に似てたから!」と謝る。
・流れている音楽に耳を傾け「君が代はいいですねぇ、僕も日本人だなぁ」と言っていたが曲は蛍の光だった。
もうお腹が捩れて涙出ます。でもちょっと個人的な趣味も手伝いこんなビデオもご紹介。
『みんな長嶋が好きだった』
これ観たらわかってもらえると思いますが、長嶋さんの影の努力は並みじゃない。裏打ちされた技術と理論によるものだったわけです。
体の使い方、脳と筋肉の関係性。これを極限まで追求したのが長嶋さんです。だから当然言葉はちぐはぐに。、、それは言葉で前頭葉(運動野)を使っていないということ。バカボン流でも同じです。運動野の言語中枢を使わず話せることが人類を人間に進化させます。
それが誰の目にもわかるから、長嶋茂雄はスーパースターなんです。そして次はジョン・レノン。
〜ジョン・レノン〜
『ジョン・レノンの名言』
長嶋さんとは好対照なジョン・レノン。言語の魔術師です。でも同じなのが前頭葉運動野に言語中枢を持っていません。残っているビデオ映像でもそれは明らか。
『ジョン・レノンのインタビュー 』
わかる人にはわかるのだけど、喋っている時に一々頭を使っていません。こころで話してる。
ジョンは音楽業界で幼少から常に抱えていた支配と自由というジレンマの証拠を掴んだ。だからこの世はキチガイに支配されてる発言もある。そしてそこには共産主義というイデオロギーが介在する。
共産主義=パリティ対称性の破れから起こる理想論。絵に書いた餅。
でもジョンはその先を観ていた。それは今オレやみんなが成すこと。もちろん👽もその中心。
こころが使える人間が現れると、世の中はパリティ対称性を保存できる客観性を持てるように変わる。それをジョンは「イマジン」で歌っている。
パリティ対称性の破れ→脳と体が離れてる。
パリティ対称性の保存→脳と体が一致。
山田塾の必須項目で、シャッフルビートを刻みながら何かを話すってのがあります。前頭葉運動野は8beat(2拍子)で駆動してます。ところが脳幹は3拍子です。そしてシャッフルビートも3拍子の仲間。つまりシャッフルビートを刻むという運動行動と、前頭葉を使って話すという運動行動にはリズム的乖離があります。だからシャッフルしながら自由に話せることには、体共鳴的な徳があるんです。もちろんジョン・レノンはできるに決まってます。もっともっと難しいビートを刻みながら自由に歌うのだから。
さあやっと情報が出揃ったようです。本格的な考察を始めましょう。
「正規分布を正しく使って寿命は伸びる」
とんでもない表題ですがどうぞご清聴くださいまし。
先ほども書いたように正規分布とは立体共鳴に於ける多数派のことです。それが言葉なら最も多くの人に伝わる意味。そして最も多くの人に伝わるということは、最も多くの人の脳と筋肉の連携とも言えます。逆説すれば世俗のトレンドとは脳と筋肉のトレンドでもあるということなのです。
だから脳と筋肉の関係性が進化、或いは退化するなら、社会も進化、或いは退化する。それを👽はpi/piと表現してます。つまりこれは数理でもあるんです。もちろん現行数学の範囲は超えるため、詳しくは👽に習いましょう。オレも生徒の一人です。
ここで脇道に逸れますが病気という状態のそもそものお話をちょっと。
病気、体や心のトラブルは何故起こるか知ってますか?
それは脳側の小さなpiと体側の大きなpiのバランス変化が全ての病気の原因です。体側の大きなpiはなるべくなるべく脳側のpiを大きくして、パリティ対称性を保存方向にしようとしたいんです。言い方変えれば、体の神さまたちが同じサイズの脳を求めているってことです。
一方脳側は、神さまたちの大きなpiが自分の小さなpiに影響しないように守ろうとするんです。それがパリティ対称性の破れ方向。これはそのまま自然免疫(神さま)と獲得免疫(人類)って意味でもあります。
そして寿命とは、このpi/piがより1に近づくに従い長くなります。つまり下界の都合と神さまの都合をつけて、1に近いほど寿命は伸びるんです。もちろん下界の都合を全く聞かず神さまの都合だけ聞いていたら、それこそ犯罪者になっちゃいます。でもその脳と神さまの関係から時間を生成し、社会を変えることができます。正規分布を変えられるんです。そうした三位一体の関係を掻い潜った人に長い寿命が与えられるわけです。それを式化するとこんなです。
蝋燭🕯=素直さ×pi/pi→素直さ=1/脳内ブレーキ
長嶋茂雄もジョン・レノンもものすごく頑張ったから、パリティ対称性が保存され、社会に多大な影響を与えたって言えます。但し長嶋さんは体を使ってつかって修行して、ジョン・レノンは運命に任せ狂弾に倒れ。だから素直に寿命換算は成り立ちませんが。
この二人のようにきっと始めはただ単に好きで野球を、バンドをしたのでしょう。そして集中して集中して、努力して努力して。いつの間にか誰にも追いつけないところまで登り詰めたことでしょう。だからこの二人の人生は前人未到の旅って言えると思います。でもこれから先の人は違います。何故なら今こそ人類が人間に進化する時だからです。
脳と体のパリティ対称性が保存されると、これまで知り得なかった体感、感覚で満たされます。そんな状況からの努力はさらに人の能力を倍増させます。例えば色温度に対する色覚細胞の相対性なども獲得できるはずです。それは確実に主観的観念論からの脱出が可能になることです。
最後にツイッターのお友達のロニさんとの話をおまけに今回の考察はこれまで。
「老害」
ロニ:なんていうか、こっちの勝手な気持ちだけど
若い頃、無茶やったり、ちょっとはぐれ者的なキャラで売ってた人が、ただの老害に成り果ててる様を見るのは、わりとオモロイ
🙃(山田):往々にしてそうなるよね。自分が突っ張っていたこと忘れちゃうんだよね。そして周りの若い芽を摘む老害と化す。
🙃:[1/突っ張る=老害]の法則ロニ:法則があるんだ!!
🙃:でもこれはパリティ対称性が破れた脳と体の関係から発生するんだよ。対称性が保存された関係からだと、例えばエリッククラプトンのように、或いはクイントイーストウッドのように、じーさんになっても突っ張り続ける。初心を忘れない。
ロニ:なるほどなるほど!!!音読しよう。イヤホン着けて歩かない!
🙃:がーさす。
ロニ:頭と体が同じことをしているって言うのが「今ここにいる」の意味だ
🙃:そういうことです。